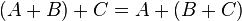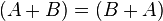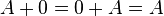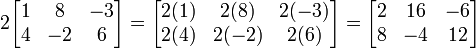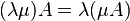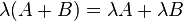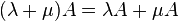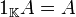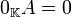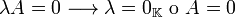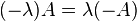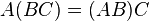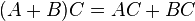OPERACIONES CON MATRICES
viernes, 26 de octubre de 2012
OPERACIONES CON MATRICES
Las operaciones que se pueden hacer con matrices provienen de sus aplicaciones, sobre todo de las aplicaciones en álgebra lineal. De ese modo las operaciones, o su forma muy particular de ser implementadas, no son únicas.
Suma o adición
Sean 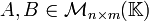 . Se define la operación de suma o adición de matrices como una operación binaria
. Se define la operación de suma o adición de matrices como una operación binaria  tal que
tal que  y donde
y donde 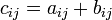 en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo
en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada 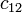 es igual a la suma de los elementos
es igual a la suma de los elementos 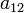 y
y 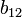 lo cual es
lo cual es 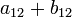 .
.
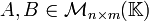 . Se define la operación de suma o adición de matrices como una operación binaria
. Se define la operación de suma o adición de matrices como una operación binaria  tal que
tal que  y donde
y donde 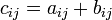 en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo
en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada 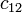 es igual a la suma de los elementos
es igual a la suma de los elementos 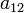 y
y 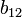 lo cual es
lo cual es 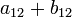 .
.
Veamos un ejemplo más explícito. Sea 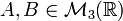
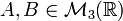
No es necesario que las matrices sean cuadradas:

A la luz de éstos ejemplos es inmediato ver que dos matrices se
pueden sumar solamente si ambas tienen el mismo tamaño. La suma de
matrices en el caso de que las entradas estén en un campo
serán la asociatividad, la conmutatividad, existencia de elemento
neutro aditivo y existencia de inverso aditivo. Ésto es así ya que éstas
son propiedades de los campos en los que están las entradas de la matriz. A continuación se presentan las propiedades.
Propiedades
- Asociatividad
Demostración. Dada la definición de la operación binaria 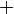 se sigue el resultado ya que
se sigue el resultado ya que  debido a que
debido a que  para todo
para todo  .
.
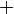 se sigue el resultado ya que
se sigue el resultado ya que  debido a que
debido a que  para todo
para todo  .
.- Conmutatividad
Demostración Dada la definición de la operación binaria 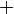 se sigue el resultado ya que
se sigue el resultado ya que  debido a que
debido a que  para todo
para todo  .
.
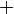 se sigue el resultado ya que
se sigue el resultado ya que  debido a que
debido a que  para todo
para todo  .
.- Existencia del elemento neutro aditivo
Existe 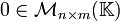 tal que
tal que
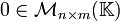 tal que
tal que
Demostración Tómese 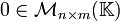 tal que
tal que  para cualquier
para cualquier  (dónde este último es el elemento neutro aditivo en el campo, el cual existe necesariamente). Entonces para cualquier
(dónde este último es el elemento neutro aditivo en el campo, el cual existe necesariamente). Entonces para cualquier 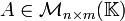 se sigue que
se sigue que 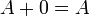 ya que
ya que  para cualquier
para cualquier  , dado que las entradas están en un campo.
, dado que las entradas están en un campo.
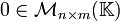 tal que
tal que  para cualquier
para cualquier  (dónde este último es el elemento neutro aditivo en el campo, el cual existe necesariamente). Entonces para cualquier
(dónde este último es el elemento neutro aditivo en el campo, el cual existe necesariamente). Entonces para cualquier 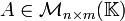 se sigue que
se sigue que 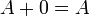 ya que
ya que  para cualquier
para cualquier  , dado que las entradas están en un campo.
, dado que las entradas están en un campo.- Existencia del inverso aditivo
Existe 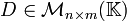 tal que
tal que
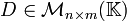 tal que
tal que
a esta matriz 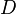 se le denota por
se le denota por 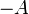 .
.
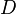 se le denota por
se le denota por 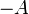 .
.
Demostración Dada 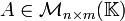 tómese
tómese 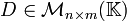 tal que
tal que  . Entonces
. Entonces  ; luego, por las propiedades de campo
; luego, por las propiedades de campo  donde
donde  es el inverso aditivo de
es el inverso aditivo de 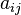 en el campo para cualquier
en el campo para cualquier  .
.
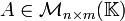 tómese
tómese 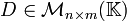 tal que
tal que  . Entonces
. Entonces  ; luego, por las propiedades de campo
; luego, por las propiedades de campo  donde
donde  es el inverso aditivo de
es el inverso aditivo de 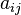 en el campo para cualquier
en el campo para cualquier  .
.En efecto, éstas propiedades dependen el conjunto en el que estén las entradas, como se ha dicho antes, aunque en las aplicaciones generalmente los campos usados son
 (los números reales) y
(los números reales) y  (los números complejos).
(los números complejos).
Por como se definió la operación binaria adición se dice que ésta operación es una operación interna por lo que se cumple intrinsecamente la propiedad de que  es cerrado bajo adición. Con éstas propiedades se tiene que
es cerrado bajo adición. Con éstas propiedades se tiene que  es un grupo abeliano.
es un grupo abeliano.
 es cerrado bajo adición. Con éstas propiedades se tiene que
es cerrado bajo adición. Con éstas propiedades se tiene que  es un grupo abeliano.
es un grupo abeliano.
En el caso en que el conjunto al que pertenecen las entradas de la matriz sea un anillo 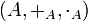 , la operación de adición de matrices continúa dotando de estructura de grupo abeliano a
, la operación de adición de matrices continúa dotando de estructura de grupo abeliano a  , ya que bajo un anillo
, ya que bajo un anillo 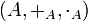 se tiene que
se tiene que 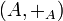 es un grupo abeliano. En el caso de que las entradas estén en un grupo
es un grupo abeliano. En el caso de que las entradas estén en un grupo 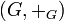 , éste necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a
, éste necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a  .
.
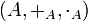 , la operación de adición de matrices continúa dotando de estructura de grupo abeliano a
, la operación de adición de matrices continúa dotando de estructura de grupo abeliano a  , ya que bajo un anillo
, ya que bajo un anillo 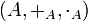 se tiene que
se tiene que 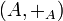 es un grupo abeliano. En el caso de que las entradas estén en un grupo
es un grupo abeliano. En el caso de que las entradas estén en un grupo 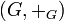 , éste necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a
, éste necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a  .
.Producto por un escalar
Sean 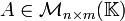 y
y 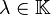 . Se define la operación de producto por un escalar como una función
. Se define la operación de producto por un escalar como una función 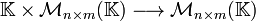 tal que
tal que  y donde
y donde 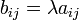 en donde el producto es la operación binaria correspondiente pero en el campo
en donde el producto es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada 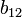 es igual al producto
es igual al producto  .
.
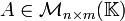 y
y 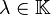 . Se define la operación de producto por un escalar como una función
. Se define la operación de producto por un escalar como una función 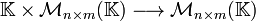 tal que
tal que  y donde
y donde 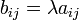 en donde el producto es la operación binaria correspondiente pero en el campo
en donde el producto es la operación binaria correspondiente pero en el campo  . Por ejemplo, la entrada
. Por ejemplo, la entrada 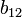 es igual al producto
es igual al producto  .
.
Veamos un ejemplo más explícito. Sea 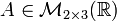 y
y 
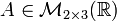 y
y 
También es inmediato observar que el producto por un escalar da como
resultado una matriz del mismo tamaño que la original. También el
producto por un escalar dependerá de la estructura algebraica en la que las entradas están. En el caso de que estén en un campo
serán dos distributividades (una respecto de suma de matrices y otra
respecto de suma en el campo), asociatividad y una propiedad
concerniente al producto por el elemento neutro multiplicativo del
campo. A continuación se presentan las propiedades.
Propiedades
Sean 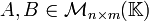 y
y 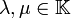 , donde
, donde  es un campo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar
es un campo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar
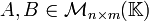 y
y 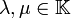 , donde
, donde  es un campo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar
es un campo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar- Asociatividad
Demostración. Dada la definición de la operación se sigue el resultado ya que 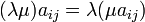 debido a que
debido a que 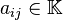 para todo
para todo  .
.
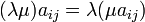 debido a que
debido a que 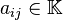 para todo
para todo  .
.- Distributividad respecto de la suma de matrices
Demostración Dada la definición de la operación se sigue el resultado ya que  debido a que
debido a que  para todo
para todo  .
.
 debido a que
debido a que  para todo
para todo  .
.- Distributividad respecto de la suma en el campo
Demostración Dada la definición de la operación se sigue el resultado ya que  debido a que
debido a que 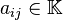 para todo
para todo  .
.
 debido a que
debido a que 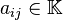 para todo
para todo  .
.- Producto por el neutro multiplicativo del campo
Demostración Dada la definición de la operación se sigue el resultado ya que  debido a que
debido a que 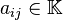 para todo
para todo  .
.
 debido a que
debido a que 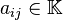 para todo
para todo  .
.Por como se definió la operación de producto por escalares se dice que
 es cerrado bajo producto por escalares. Con éstas propiedades y las de la adición se tiene que
es cerrado bajo producto por escalares. Con éstas propiedades y las de la adición se tiene que  es un espacio vectorial con las operaciones de suma y producto por escalares definidas antes.
es un espacio vectorial con las operaciones de suma y producto por escalares definidas antes.
En el caso de que las entradas y los escalares no estén en un campo sino en un anillo entonces no necesariamente existe el neutro multiplicativo. En caso de que exista, con lo cual el anillo es un anillo con uno, se dice que  es un módulo sobre
es un módulo sobre  .
.
 es un módulo sobre
es un módulo sobre  .
.Ahora, a partir de las propiedades básicas se puede demostrar inmediatamente que
Demostración Dada la definición de la operación se sigue el resultado ya que 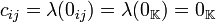 para todo
para todo  .
.
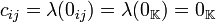 para todo
para todo  .
.
Demostración Dada la definición de la operación se sigue el resultado ya que  para todo
para todo  debido a que
debido a que 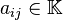 para todo
para todo  .
.
 para todo
para todo  debido a que
debido a que 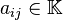 para todo
para todo  .
.
Demostración Dada la definición de la operación se sigue el resultado ya que como en un campo no hay divisores de cero entonces  para todo
para todo  implica que
implica que  o
o  para todo
para todo  , i.e.
, i.e.  .
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
.
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
 para todo
para todo  implica que
implica que  o
o  para todo
para todo  , i.e.
, i.e.  .
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
.
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
Demostración Dada la definición de la operación se sigue el resultado ya que  debido a que
debido a que 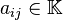 para todo
para todo  .
.
 debido a que
debido a que 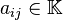 para todo
para todo  .
.
Este último resultado permite usar la notación 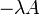 sin riesgo de ambigüedad.
sin riesgo de ambigüedad.
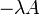 sin riesgo de ambigüedad.
sin riesgo de ambigüedad.Producto
 y
y  dando como resultado la matriz
dando como resultado la matriz  .
.
Artículo principal: Multiplicación de matrices.
Artículo principal: Aplicación lineal.
El producto de matrices se define de una manera muy peculiar y hasta
caprichosa cuando no se conoce su origen. El origen proviene del papel
de las matrices como representaciones de aplicaciones lineales.
Así el producto de matrices, como se define, proviene de la composición
de aplicaciones lineales. En este contexto, el tamaño de la matriz
corresponde con las dimensiones de los espacios vectoriales
entre los cuales se establece la aplicación lineal. De ese modo el
producto de matrices, representa la composición de aplicaciones
lineales.
En efecto, en ciertas bases tenemos que  se puede representar como
se puede representar como  donde
donde 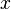 es la representación de un vector de
es la representación de un vector de 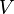 en la base que se ha elegido para
en la base que se ha elegido para 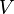 en forma de vector columna. Si tenemos dos aplicaciones lineales
en forma de vector columna. Si tenemos dos aplicaciones lineales  y
y 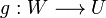 entonces
entonces  y
y 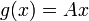 , luego la aplicación
, luego la aplicación 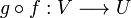 se representará como
se representará como 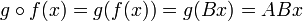 donde
donde  es el producto de las representaciones matriciales de
es el producto de las representaciones matriciales de 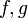 . Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de
. Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de 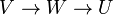 ,
en particular debe de haber una relación entre las dimensiones de los
espacios vectoriales. Una vez dicho ésto podemos definir el producto de
la siguiente manera.
,
en particular debe de haber una relación entre las dimensiones de los
espacios vectoriales. Una vez dicho ésto podemos definir el producto de
la siguiente manera.
 se puede representar como
se puede representar como  donde
donde 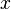 es la representación de un vector de
es la representación de un vector de 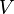 en la base que se ha elegido para
en la base que se ha elegido para 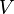 en forma de vector columna. Si tenemos dos aplicaciones lineales
en forma de vector columna. Si tenemos dos aplicaciones lineales  y
y 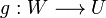 entonces
entonces  y
y 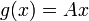 , luego la aplicación
, luego la aplicación 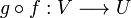 se representará como
se representará como 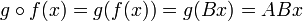 donde
donde  es el producto de las representaciones matriciales de
es el producto de las representaciones matriciales de 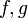 . Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de
. Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de 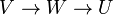 ,
en particular debe de haber una relación entre las dimensiones de los
espacios vectoriales. Una vez dicho ésto podemos definir el producto de
la siguiente manera.
,
en particular debe de haber una relación entre las dimensiones de los
espacios vectoriales. Una vez dicho ésto podemos definir el producto de
la siguiente manera.
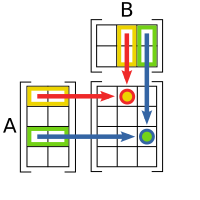
Sean 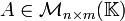 y
y 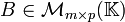 . Se define el producto de matrices como una función
. Se define el producto de matrices como una función 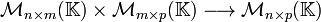 tal que
tal que  y donde
y donde 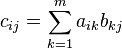 para toda
para toda  , es decir
, es decir 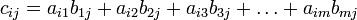 . Por ejemplo, la entrada
. Por ejemplo, la entrada 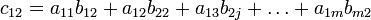 .
.
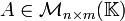 y
y 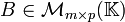 . Se define el producto de matrices como una función
. Se define el producto de matrices como una función 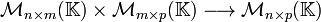 tal que
tal que  y donde
y donde 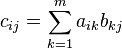 para toda
para toda  , es decir
, es decir 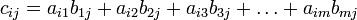 . Por ejemplo, la entrada
. Por ejemplo, la entrada 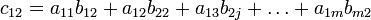 .
.
Veamos un ejemplo más explícito. Sean 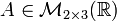 y
y 
 y
y 
dónde la matriz producto es como habíamos establecido en la definición: una matriz  .
.
 .
.
Sin tomar en cuenta la motivación que viene desde las aplicaciones
lineales, es evidente ver que si ignoramos la definición de la función
de producto de matrices y sólo se toma en cuenta la definición de las
entradas, el producto no estará bien definido, ya que si  no tiene el mismo número de columnas que
no tiene el mismo número de columnas que  de filas entonces no podremos establecer en donde acaba la suma: si la
acabamos en el mayor de éstos números habrá sumandos que no están
definidos ya que una de las matrices no tendrá mas entradas, mientras
que si tomamos el menor habrá entradas de alguna de las matrices que no
se tomen en cuenta. Así es necesario que
de filas entonces no podremos establecer en donde acaba la suma: si la
acabamos en el mayor de éstos números habrá sumandos que no están
definidos ya que una de las matrices no tendrá mas entradas, mientras
que si tomamos el menor habrá entradas de alguna de las matrices que no
se tomen en cuenta. Así es necesario que  tenga el mismo número de columnas que
tenga el mismo número de columnas que  de filas para que
de filas para que  exista.
exista.
 no tiene el mismo número de columnas que
no tiene el mismo número de columnas que  de filas entonces no podremos establecer en donde acaba la suma: si la
acabamos en el mayor de éstos números habrá sumandos que no están
definidos ya que una de las matrices no tendrá mas entradas, mientras
que si tomamos el menor habrá entradas de alguna de las matrices que no
se tomen en cuenta. Así es necesario que
de filas entonces no podremos establecer en donde acaba la suma: si la
acabamos en el mayor de éstos números habrá sumandos que no están
definidos ya que una de las matrices no tendrá mas entradas, mientras
que si tomamos el menor habrá entradas de alguna de las matrices que no
se tomen en cuenta. Así es necesario que  tenga el mismo número de columnas que
tenga el mismo número de columnas que  de filas para que
de filas para que  exista.
exista.
Como se puede suponer también, las propiedades de ésta operación
serán más limitadas en la generalidad ya que además de las limitaciones
impuestas por la naturaleza de las entradas está esta limitación
respecto a tamaño. Es claro, además, que el producto de matrices no
siempre es una operación interna.
Propiedades
Sean  matrices con entradas en
matrices con entradas en  , donde
, donde  es un campo, entonces se cumplen las siguientes propiedades para el
producto de matrices (considerando que los productos existan)
es un campo, entonces se cumplen las siguientes propiedades para el
producto de matrices (considerando que los productos existan)
 matrices con entradas en
matrices con entradas en  , donde
, donde  es un campo, entonces se cumplen las siguientes propiedades para el
producto de matrices (considerando que los productos existan)
es un campo, entonces se cumplen las siguientes propiedades para el
producto de matrices (considerando que los productos existan)- Asociatividad
Demostración. Dada la definición de la operación se sigue el resultado ya que, si  ,
,  y
y  por lo que
por lo que 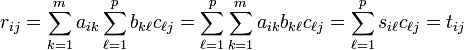 donde
donde  debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 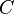 es
es  .
.
 ,
,  y
y  por lo que
por lo que 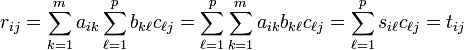 donde
donde  debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 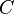 es
es  .
.- Distributividad respecto de la suma de matrices por la derecha
Demostración Dada la definición de la operación se sigue el resultado ya que 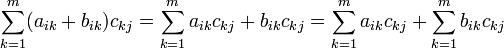 debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 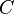 es
es  .
.
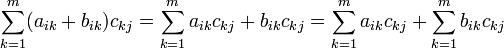 debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 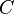 es
es  .
.- Distributividad respecto de la suma de matrices por la izquierda
Demostración Dada la definición de la operación se sigue el resultado ya que 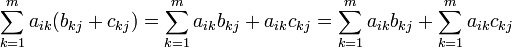 debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 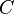 es
es  .
.
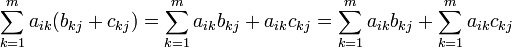 debido a que
debido a que  para todo
para todo  . Aquí estamos considerando que
. Aquí estamos considerando que  es
es  ,
,  es
es  y
y 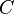 es
es  .
.El producto de matrices no es conmutativo, si lo fuera la composición de funciones lineales sería conmutativa y eso en general no sucede. Obviamente existen casos particulares de algunos tipos de matrices en los que si hay conmutatividad. En el caso en que tengamos
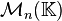 tendremos que el producto entre matrices en
tendremos que el producto entre matrices en 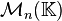 también está en
también está en 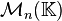 . En ese caso
. En ese caso 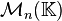 además de espacio vectorial es un álgebra sobre un campo. En el caso de que el conjunto al que pertenecen las entradas sea un anillo conmutativo con uno entonces
además de espacio vectorial es un álgebra sobre un campo. En el caso de que el conjunto al que pertenecen las entradas sea un anillo conmutativo con uno entonces  además de módulo es un álgebra sobre un anillo. Mas aún
además de módulo es un álgebra sobre un anillo. Mas aún  con
con  el producto de matrices es un anillo.
el producto de matrices es un anillo.Rango
Artículo principal: Rango de una matriz.
El rango de una matriz  es la dimensión de la imagen de la aplicación lineal representada por
es la dimensión de la imagen de la aplicación lineal representada por  , que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de
, que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de  .
.
 es la dimensión de la imagen de la aplicación lineal representada por
es la dimensión de la imagen de la aplicación lineal representada por  , que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de
, que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de  .
.Traspuesta
Artículo principal: Matriz traspuesta.
La traspuesta de una matriz 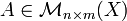 , donde
, donde  no es necesariamente un campo, es una matriz
no es necesariamente un campo, es una matriz 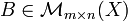 tal que
tal que 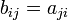 . Por ejemplo la entrada
. Por ejemplo la entrada 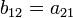 .
.
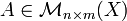 , donde
, donde  no es necesariamente un campo, es una matriz
no es necesariamente un campo, es una matriz 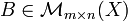 tal que
tal que 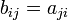 . Por ejemplo la entrada
. Por ejemplo la entrada 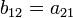 .
.
Veamos un ejemplo más explícito. Sea 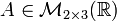
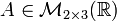
entonces su traspuesta es
Así, informalmente podríamos decir que la traspuesta es aquella
matriz que se obtiene de la original cambiando filas por columnas. Las
notaciones usuales para denotar la traspuesta de una matriz son 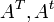 .
.
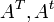 .
.
La trasposición de matrices tiene las siguientes propiedades (donde
ahora si el conjunto de entradas debe ser al menos un anillo
conmutativo):
Si 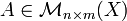 representa una aplicación lineal, entonces la matriz
representa una aplicación lineal, entonces la matriz  describe la traspuesta de la aplicación lineal.
describe la traspuesta de la aplicación lineal.
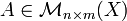 representa una aplicación lineal, entonces la matriz
representa una aplicación lineal, entonces la matriz  describe la traspuesta de la aplicación lineal.
describe la traspuesta de la aplicación lineal.
Suscribirse a:
Entradas (Atom)
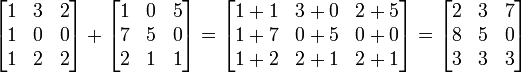
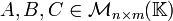 , donde
, donde